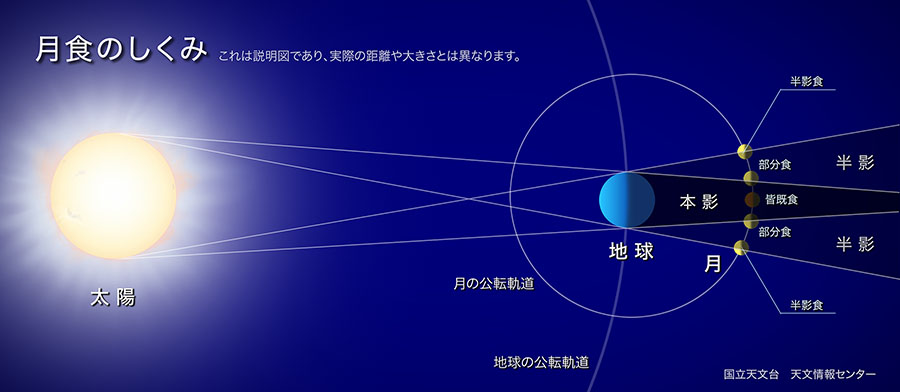
このブログは子供向けです。子供向けですが、どこにも負けない科学的な月蝕分析を行っています。
(画像は国立天文台のホームページから借用しています)
さて、月食のことはどれほど知っていますか。
月食のことを少し知っている小さい小学生に聞くと「月が地球の影に入って暗くなること。」と、易しく答えてくれます。
もう少し知っている高学年に聞くと「太陽、地球、月が一直線に並ぶと、月が地球の影に入ってしまい、暗くなる。通常赤っぽい色になる。このような天文現象のこと。」と、レベルの高い答えが帰ってきます。
これらのことを科学的に考察してみるとどうなるのでしょうか。
1.太陽、地球、月が一直線とはどのようなことか。
2.月が地球の影に入るとはどのようなことか。
3.赤っぽい色とはどのようなことか。
実は、このブログを書き出して、2つの発見がありました。(発見は大げさですけど)
一つは、夜に関して。夜は何でしょうか。地球は球体であり、太陽に向いていない方の半球には太陽光が当たらなくて暗くなり、それが夜と名付けられています。太陽光が当たらないと言うことの意味は、地球の半分が影を作っていて、その影に入った半分が暗くなり、夜と呼ばれていることになります。太陽光が当たらない意味は、球体の半分が影を作っているからだと思い当たりました。
もう一つは、宇宙空間にも影が存在しているのだと、いまさらながら、勝手に感動しました。太陽系にいくつかの円錐形の影が存在しているところを想像してみてください。ちょっと面白い太陽系になりませんか。普段気づかない太陽系の影を月蝕や日蝕が気づかせてくれます。ただ、宇宙空間の影はそのままでは見えません。光(色)も見えませんけど。
閑話休題
では、一番目の一直線と二番目の地球の影から考察して行きましょう。
紙の上に直線を書いて、その上に左から太陽、地球、月の円を書いてみましょう。3つの天体が一直線に並びました。これで、月食になる条件が整いました。左の太陽の円から光が右へ向けって進むと、確かに地球が光を遮って月には光が届きません。めでたく月食です。
続いて、この3つの天体を目の前の空間に浮かべてみましょう。浮かんでいる状態を想像してみましょう。どうでしょうか、目の前の3次元空間に浮いた太陽、地球、月も一直線に並んで、月食が起こっていますね。宇宙空間のシミュレーションも成功です。
さて、今回の皆既月食は、欠け始めが18:45、欠けのない状態になるのが21:52です。3時間程ですが、この3時間は、天体が動いているために現れる現象にかかわる時間です。
3つの天体は宇宙空間で全て動いています。ちなみに太陽系は銀河系の周りを時速84万キロという猛烈はスピードで動いています。地球は太陽の周りを時速10万キロで動いています。月は地球の周りを時速3600キロで回っています。遅いですね。3つの天体の動きは月食にどのように影響するのでしょうか。
月食を考えるときには、実は、上記の速度はこけおどしでしかありません。太陽、地球、月は同じ太陽系に乗っていますので、同じ電車に乗っている人が車内でのお互いの動きには電車の速度は無関係なのと同じく、3つの天体の太陽系内での動きに対して、太陽系の速度は無視できます。よかった。
さて、太陽系の中では、惑星は太陽を中心としてその周りを回っています。上記のように、地球は時速10万キロという猛スピードです。この猛スピードで今回の月食時間である3時間動くとどれほど位置が変わるでしょうか。
分かりやすくするために、ここで角度を使います。地球は365日で太陽を一回り360度進みます。一日約1度です。月食の3時間では、0.125度。ノートの上に分度器で1度の1/8の角度を書いてみて下さい。ほぼ無理ですね。地球は3時間ではほとんど動かないとみてよさそうです。
最後に月ですが、月は27.3日で地球を一周します。(27.3日は恒星月、暦で使う29.5日は朔望月。違いの説明は別の機会に)。そうすると、3時間では、1.65度進みます。地球の0.125度は1.65度の7.6%ほどでしかありません。
ここまでの3つの惑星の動きを考えると、月食中の3時間の動きは、ほぼ月の動きで生じる現象と言うことができます。
ここまで、いいですか。
ここでは月の大きさを測る事はしませんが、月食を利用すると月の大きさを測ることが出来ます。それは、またの機会に譲りましょう。
次に進む前に、一旦月食を離れて日食を考えてみたいと思います。日食の情報は月食を考えるうえで大いに役立ちます。
皆既日食の時、月が地球上につくる影は惑星などのサイズと比較すると、ほぼ点と考えられます。月の直径は3474Km、地球と月の距離は平均38万キロ。つまり、38万キロ離れると、直径3474Kmの円の影がゼロになることを現わしています。
上記の数値は、月食を考えていくうえで、大変役立つ情報です。
つまり直径12742Kmの地球が作る影は、地球から38万キロ離れた地点では、月の直径分小さい9268Kmの直径の影になっていることが導かれます。この地点でのこの影の大きさは、月2.7個分に相当します。
さて、今回の月食は欠け始めから欠け終わりまで3時間です。
3時間かけて、直径9280Kmの影を潜り抜けようとすると何が起こるでしょうか。
ノートの1ページの真ん中に大きい円を一つ描いてください。その中心を通る直線を一本引きます。続いて、小さい円を3つ大きい円の内側に直線の上に並べて書いてください。3つとも円の内側ではなく、3つ目は7割が円の内側3割が円の外側になるように、並べて書きます。
これで、影の大きさが月の大きさの2.7個分の地球の影と、地球から38万キロ離れた月が、中心線に沿って描けました。
追加で、3つの小さい円の左右に小さい円を描いておきましょう。
実は、月の視直径はおおよそ0.52度です。月の動く量は1時間で0.55度です。つまり、上に描いた小さい円つまり月は、38万キロかなたにあって地球から見ていると1時間で月1個分動く計算です。では、先ほどの大きい円と5つの小さい円を見てください。地球の影の中心を月が通っている図になります。月が影に入り始めて、完全に出るまでのおおよその時間を算出してみましょう。左端の月が右に1つ分動くと1時間です。もう一つ動いて2時間、もう一つ動いて3時間。おやおや、3時間後に地球の影から完全には出ていませんね。
このことの意味は、もう分かりますね。今回の月は、影の中心から少し外れたコースを通って行きます。中心を通る場合は、あと40分ほど余分にかかることになります。
ここまでは、いいですか。
一直線に関連して、もう一つ重要な考察があります。
太陽、地球、月がこの順番に一直線に並ぶと思われるケースで、満月があります。満月はほぼ毎月1回起こりますが、月食にならない場合がほとんどです。月食なら満月であるという十分条件だけが成立し必要条件は成立しません。
太陽、地球、月がこの順番に一直線に並べば月食。この文は必要十分条件になっています。下記のような表現もできます。
一直線←月食←満月 〇 X
一直線→月食→満月 〇 〇
満月なのに、月食になったりならなかったりする理由は何でしょうか。上記の必要十分条件から、満月ではあるけれども、一直線に並んでいないから月食にならないということが導き出されてきます。一直線でないなら、太陽と地球を結ぶ線と地球と月を結ぶ線が90度に交わっていたらどうでしょう。この場合は、そもそも半月であり満月ではありませんから、考える必要はないことになります。
満月なのに月食でない理由は、一直線に並んで見えるけれども実際は一直線ではないことを意味します。疑似一直線と名付けましょうか。
なぜ本物の一直線と疑似一直線が生じるのでしょうか。太陽と地球と月の軌道面の研究・観察から月の軌道面は太陽-地球の軌道面に対して5.1度傾いていることが分かっています。満月は2次元的には一直線に思えても、3次元的には必ずしも、一直線ではなく最大5.1度上下にずれた位置にいるために、月食になならないことになるのです。
軌道面が傾いていることが原因だと分かりました。今、月が5.1度軌道面より上にあるところから、地球が太陽を周り始めると、地球は一年間に一回太陽を回りますから、3ケ月後には月の軌道面が地球の軌道面と0度の所に来ます。その3ケ月後には、5.1度下に来ます。さらに3ケ月後にはまた0度の位置に来ます。1年経つともとに戻って5.1度上の位置に来ます。
つまり、3次元的に一直線に並ぶのは、半年に一度ということになります。実際おおよそ6ケ月ごとに月食(皆既か部分かわ問わず)が起こります。
ただし、月は8.85年で一周する近点移動(また、別の機会に学びましょう)を起こすために、6ケ月ごととはならずに、周期に乱れが生じます。
2021/5/26皆既、2021/11/19部分、2022/5/16皆既、2022/11/8皆既、2023/10/29部分、2024/9/18部分、2025/3/14皆既。このように時々乱れます。
ここまでいいですか
上でも既に言及していますが、地球の影に入るとはどのようなことか、追加で少し考察をしていきましょう。
月の軌道面は地球の軌道面に対して5.1度傾いていると上で書きました。38万km離れた地点で、tan5.1°を計算すると、33,820kmになります。38万kmの地点での影の大きさは直径9,268km、半径で4,634kmでしたから、軌道面が最大に傾いた状態での月の位置は、地球の影から3万キロ程離れた場所になります。月食にはほど遠いことになります。
最後に、赤っぽい色を考察していきましょう。
地球が作る影には、本影と呼ばれる濃い影とそれを取り巻く半影と呼ばれる薄い影があります。薄い影の部分を月が通るときは半影月食と呼びますが、余り目だった変化はありません。
皆既月食、部分月食は本影の中を月が通過するときの現象です。
通常私たちが目にする、太陽による影は黒くなっています。赤いライトに照らされても影は黒くなります。しかるに、月食中の月は赤っぽくなります。なぜでしょうか。
ヒントは、朝焼け、夕焼け、日の出、日の入りにあります。朝焼け、夕焼けは、空がオレンジっぽくなります。太陽も、南中している時は白っぽい黄色で輝いていますが、日の出や日の入りの時はオレンジっぽく見えます。
理由は光が通過する大気の距離と光の散乱の仕方にあります。
昼間上方に太陽が位置する場合は、光は大気の厚さ100kmを通過してきます。この大気の厚さだとレイリ散乱(波長より小さい粒子に当たって光が散乱される時の原理、波長の4乗に逆比例)により、波長の短い青い光が大気中で何度も何度も散乱され我々の目に入ってきます。青い光の波長は赤い光の波長のおおよそ半分ですから、赤い光は青い光の16分の1しか大気中で散乱されてきません。よって、空は青く見えます。
青い波長の光だけが散乱されて届くのなら、地球全体が青くならないのでしょうか。なりません。地球に届く光の大部分は、散乱されずに直接地上まで届いているため、青くもなりませんし、暗くもなりません。
さて、日の出と日の入はどうでしょうか。日の出日の入の時太陽が水平線や地平線方向から太陽光がやって来るとします。そうすると太陽光は真上に比べてずいぶん長い距離、大気の中を進むことになります。実はその距離がどれくらいかネットで調べたのですが、全て「かなり長い」「大変長い」「はるかに長い」のような表現だけしかしていません。こんなのでは科学の名折れです。
そこで、ここではちゃんと計算しました。計算方法自体は実は簡単です。考え方次第です。計算結果は、大気の22倍2200kmにもなります。
これだけの長さを通過すると、青い光は散乱しすぎて、もう我々の元へは届かなくなります。何kmが限度かは計算していません。
一方、赤い光は、散乱が少ないため、2200kmの距離を通過しても、我々のもとへ届きます。光は面白いですね。
ここまではいいですか。
いよいよ最終コーナーです。先ほど本影と半影があると言いました。半径3cmを左に半径1cmの円を右に、5cmくらい離して描いて、太陽と地球の接線を4本描いてみてください。内側の2本に囲まれた領域が本影、外側の2本で囲まれた2領域が半影になります。
本影に入った月が赤っぽく見えるという事は、本影の中に波長の長い赤系統の光が紛れ込んでいるのだろうと想像できます。なんとなく日の出日の入の現象で説明が付きそうな気がしませんか。
今描いた図を見ると、大気の層を通過する赤い光は、本影の周辺のほんの僅かな部分にだけしか存在しない事が分かります。残念ながら、日の出日の入の現象だけでは説明がつきません。
先ほどの4本の接線をもう一度見てみましょう。接線は直線です。赤系統の光はその直線の内側に曲がって入って行ったことになります。宇宙に反射する鏡があるわけではないので、光が屈折を起こして内側に入って行ったことになります。
光の屈折とくれば、空気中と水中の光の曲がりを確かめる実験がよくありますが、皆さんも一度は実験をされたことでしょう。
光は、通過する物質の性質により、いろいろな屈折率で屈折します。水の屈折率は1.333、60度で入射すると41度と見た目にもはっきりとわかるほど大きく屈折します。では空気はどうでしょうか。空気の屈折率は1.0003。ほとんど曲がりません。この屈折率では赤系統の光が本影に入り込むような現象にはなりません。アレレ、期待外れ?
大気の成分は、窒素78%、酸素21%、アルゴン0.9%、二酸化炭素0.032%、その他。幸いなことに、大気中には水が蒸発した水蒸気と、雲の状態になった氷の粒が存在していて、大気としての屈折率がおおよそ、1.006と純粋の空気より20倍も曲がりやすくなっています。この屈折率ですと、34分(約0.5°)も曲がります。
ありがたいことに、さらに、光が大気に入るときに曲がり、大気を出る時にも曲がります。2回合わせて1度以上屈折します。これだけ曲がると、月が通る地球から38万キロの地点で完璧に赤系統の光が月を照らすことになります。
天文学では、この屈折を大気差と呼んでいます。地平線に隠れているはずの星が地平線より上にあるように見える現象も大気差のおかげです。ただし、大気差の屈折は入射角によってずいぶん変化します。0度(水平線・地平線ギリギリ)で入射の時は屈折は34分ありますが、5度では10分、10度では5分、45度では1分と小さくなります。
いかがだったでしょうか。長文になりましたが、不明な点はお尋ねください。